Bond Duration Guide: Definitions, Concepts and Examples
Bond duration is a key concept in investment management and corporate finance that allows investors and financial professionals to measure the sensitivity of a bond’s price to changes in interest rates. Understanding duration is crucial for assessing the amount of risk associated with a bond investment and for structuring bond portfolios to achieve specific investment objectives.
Article Contents
Key Takeaways
| Concept | Description |
| Bond Duration | Measures the sensitivity of a bond’s price to changes in interest rates, assessing risk and guiding portfolio structure. |
| Types of Duration | Macaulay Duration: Weighted average time until a bondholder receives cash flows. Unit of measurement: time (years)
Modified Duration: Measures bond price sensitivity to interest rate changes across the yield curve (i.e. a shift in rates for all maturities – see Key Rate Duration below, in contrast) Unit of measurement: % Effective Duration: For bonds with options, adjusts for potential changes in cash flows. Dollar Duration: Measures dollar change in bond price for a percentage interest rate change. PV01: is a sub-set of Dollar Duration, measuring the price change of a bond resulting from a 1bp (0.01%) change in rates Key Rate Duration: Measures sensitivity to yield curve changes at specific maturities, rather than all maturities |
| Calculating Duration | Utilizes various formulas to determine different types of durations – see below for an Excel example |
| What is a ‘Good’ Bond Duration | This varies depending upon the context. Short durations are preferred in rising interest rate environments; longer durations beneficial when rates are expected to fall. |
| Short-term Bonds and Duration | Short-term bonds have a maturity of 5 years or less and are less sensitive to interest rate changes but offer lower yields. |
| Duration Risk | Higher duration gives higher interest rate sensitivity, all other things being equal. This can be managed through diversified bond portfolios and hedging strategies. |
| Practical Applications | Used to compare interest rate risks, match bond portfolio durations with liabilities, employ bond immunisation strategies, assess bond yields versus risks, and hedge against duration risk. |
| Examples for Calculation | Below, you will find examples on the calculation of Macauley Duration and Modified Duration. |
What is Bond Duration?
Bond duration, in its simplest sense, measures the average time period it will take, in years, for an investor to be repaid the bond’s price by the bond’s total cash flows. In other words, duration is the weighted average life of a bond’s cash flows, taking the time value of money into account.
The amazing thing is that this same measure of duration Is very close to being the % change in a bond’s price resulting from a 100bp (1%) change in yield on that bond. A higher duration means the bond’s price is more sensitive to yield changes, whilst a lower duration means the bond’s price is less sensitive.
Types of Bond Duration
Understanding the various types of bond duration is crucial for investors seeking to manage the interest rate risk inherent in fixed-income investments. Here are the most commonly used duration types:
Macaulay Duration
Macaulay Duration, named after Frederick Macaulay who introduced the concept, is the weighted average time until a bondholder receives the bond’s cash flows. It is a fundamental measure used to determine the sensitivity of a bond’s price to interest rate changes. The Macaulay Duration is calculated by summing the present values of all cash flows, each multiplied by the time until receipt, and then dividing by the current bond price.
Modified Duration
Modified Duration is a derivative of Macaulay Duration and provides a direct measure of a bond’s price sensitivity to interest rate changes. It is calculated by dividing the Macaulay Duration by one plus the yield to maturity per period. This adjustment transforms the Macaulay Duration into an elasticity measure, estimating the percentage change in price for a 1% change in yield.
Effective Duration
Effective Duration is particularly relevant for bonds with embedded options, like callable or putable bonds. It considers potential changes in cash flows due to these options. Effective Duration is calculated under the assumption that the bond’s cash flows may change as interest rates change, providing a more accurate measure of interest rate risk for these types of bonds.
Dollar Duration
Dollar Duration measures the actual dollar change in a bond’s price for a one percentage point change in interest rates. It is the product of a bond’s modified duration and its price. This metric is useful for investors who wish to understand the change in their portfolio’s value in monetary terms, rather than in percentage or years.
Key Rate Duration
Key Rate Duration assesses a bond’s sensitivity to changes in the yield curve at specific maturities. For example, it can measure the change in a bond’s price in response to a 1% change in the yield for 5-year Treasury bonds. This type of duration is important for gauging the impact of non-parallel shifts in the yield curve.
Calculating Bond Duration
Macaulay Duration Formula
The most commonly used formula for calculating bond duration is the Macaulay duration:
Macaulay Duration = (t*CF)/[(1+y)^t]
Where:
- t = the time period of the cash flow
- CF = the cash flow amount at time t
- i = the periodic yield on the bond
This formula sums the present values of each individual cash flow, weighted by the timing of the cash flow. The result is expressed in years.
Modified Duration Formula
Modified Duration is equal to Macaulay Duration divided by one plus the yield to maturity divided by the number of compounding periods per year:
Modified Duration = Macaulay Duration / (1 + (Yield to Maturity / Number of Compounding Periods per Year))
There is no intuitive link here, but some simple calculus on a bond price expression could get us there. Here’s we’ll spare you the pain of going back to school with differentiation but get in touch with us and we’ll send you the simple proof!
Key Rate Duration Formula
Key Rate Duration for a specific maturity is calculated by taking the percentage change in the bond’s price and dividing it by a small change in the yield for that maturity.
Key Rate Duration at specific maturity = (Change in Price / Initial Price) / Change in Yield at that Maturity
Dollar Duration Formula
Dollar Duration is calculated by multiplying the Modified Duration by the bond’s price and then by 0.01:
Dollar Duration = Modified Duration * Bond Price * 0.01
Good Bond Duration: What Does It Mean?
“Good” bond duration depends on the investment context.
For example, in a falling rate environment, bond prices will rise. Wouldn’t it be nice to invest in bonds that responded more to that fall in rate? That would be long Duration bonds! The converse is true in a rising rate environment. What you will find is that portfolio managers will shorten the duration of their portfolios in anticipation of rates rising.
Have a look at a bond fund fact sheet (you can find one at many investment manager websites – e.g. BlackRock) and see how the duration of the portfolio compares to the benchmark – it is likely to be shown, but not always.
Short-term Bonds and Duration
By ‘short-term’ we commonly mean bonds with a maturity of 5 years or less. But there is no fixed interpretation. A bond can never have Duration any longer than its maturity. For a coupon-paying bond, the Duration will always be less than its maturity.
So, as well as shorter maturity, short-term bonds will have lower duration than any longer-term bond, and thus be less risky than longer maturity bonds, as their prices are less sensitive to interest rate changes.
However, short duration bonds typically have lower yields compared to longer maturity bonds. So any given change in rates will have a proportionately larger impact.
Remember that Duration does not measure the likelihood of any change in rates, it purely measures the impact should rates change.
It is worth noting that, although short-term bonds have lower rate sensitivity, short term rates can be more volatile. Duration does not take into account the likelihood of rate movements – it is purely a measure of “if rates change, this tells you how sensitive your bond investment(s) is.
Duration Risk: Protecting Your Investments
Duration indicates the interest rate risk inherent in a bond investment. Bonds with higher durations involve more risk, as their prices will fluctuate more widely with interest rate shifts.
Investors can manage duration risk by constructing a bond portfolio with an overall optimal duration fitting their risk tolerance and market outlook. This often involves holding bonds with a range of individual durations.
Duration risk can also be addressed through the use of bond futures, interest rate swaps, and other hedging strategies. Reducing a portfolio’s duration means reducing its sensitivity to the potentially negative impact of rising interest rates.
Practical Applications in Investment Strategies
Understanding duration has several applications for fixed income investing:
- It is a measure for comparing the interest rate risks of bonds with differing maturities and coupon rates.
- Bond portfolio durations can be matched with liability durations to manage risk flows – known as bond immunisation
- Investors should assess if a bond’s yield justifies its duration risk.
- Duration is a factor in selecting bond funds. Funds are often classified as short term or long term, based on weighted average life and Duration of the fund. If you think rates will fall, loner duration is a more appropriate investment, all other things being equal.
- Derivatives such as interest rate swaps can hedge against duration risk.
- Duration can predict approximate bond price changes for specific interest rate shifts.
Exercises and Examples for Bond Duration
Let’s look at some step-by-step examples of computing duration using the formulas discussed earlier:
Example 1:
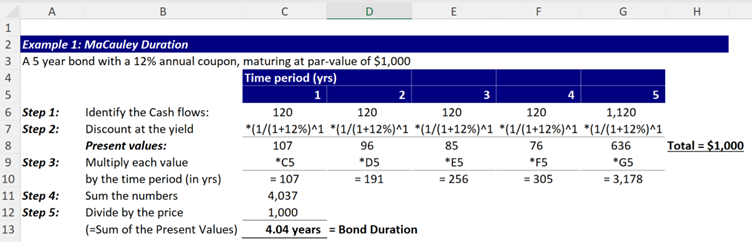
Calculate the Macaulay duration of a 5-year bond with a 12% annual coupon rate and a $1,000 face value.
Assume the current market price is also $1,000 – what is the modified duration? Use this to estimate the change in value if rates increase by 50bp.
Then we can use this to determine the modified Duration (the % change in bond price, given a 100bp change in yield):
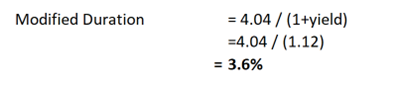
So, if rates increase by 50bp, from 12% to 12.5%, the approximate change in value is:
- 6% * Current price
- = 3.6% * $1,000
- = $36.
So the new price should be approximately $1000 – $36 = $964.
In fact, if we discount the bond cashflows at the new yield of 12.5% we get $982. This is quite some ‘rounding error’!
What you find is that, in fact, Duration is only a good measure of the change in value of the bond price for SLIGHT changes in rates.
This is because it measures sensitivity of the bond price at a single (current) yield. As soon as rates move, not only does the price change, but so does the Duration.
So to work out the true change in bond price we need firstly to measure Duration, then the rate of change of Duration as rates move! This ‘rate of change of Duration’ is known as Bond Convexity.
Example 2:
A 10-year semi-annual coupon bond has a 6% coupon rate and 8% yield to maturity. What is its approximate Macaulay duration?
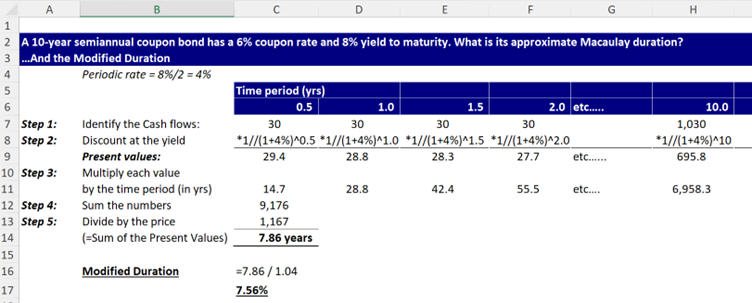
These examples demonstrate how to calculate bond duration based on the timing and size of its cash flows. The duration metric provides critical insights for managing bond interest rate risk.
In summary, duration is a key tool for measuring interest rate risk, constructing bond portfolios, and implementing bond investing strategies. The accurate calculation and interpretation of duration can help investors reach their desired risk-return profile.
Example 3:
What are the three primary factors driving the Duration of a bond?
Well, take these illustrations:
- 2 bonds with the same coupon, in the same currency but with different maturities. The longer-maturity bond will have a higher duration and be more sensitive to changing rates.
- Why? With the same coupon in the same market (currency) then the only difference is maturity. Calculating the weighted average life of a bond’s cashflows, then longer term bond MUST have a higher duration!
- 2 bonds of the SAME maturity, in the same currency, but with different coupons. The bond with the LOWER coupon will have HIGHER duration!
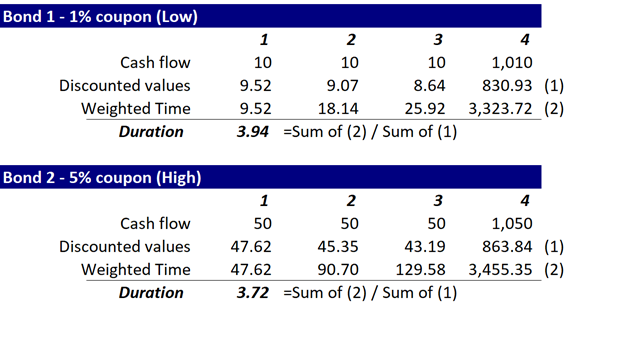
- Why? If the coupons are lower, keeping in mind that the size of the coupon becomes the weighting for the ‘time’ variable in our computation, then lower coupons means less weighting to the shorter time periods. Try it in Excel – here’s an illustration of two 4-year bonds, with yields at 5%, one with a 1% coupon, one with a 5% coupon:
- Why? If the coupons are lower, keeping in mind that the size of the coupon becomes the weighting for the ‘time’ variable in our computation, then lower coupons means less weighting to the shorter time periods. Try it in Excel – here’s an illustration of two 4-year bonds, with yields at 5%, one with a 1% coupon, one with a 5% coupon:
- Two bonds that are identical other than currency. One is in US$ where yields are 5%, the other is in the UK where yields are 8%.
- Note that Duration measures sensitivity of the price to an absolute change in rates – for example, 50bps or basis points.
- If rates for each of these bonds changed by 50bps (0.5%) that is a 10% relative change for the US$ bond (0.5% / 5%) but only a 6.25% change in rates for the UK bond (0.5% / 8%). The impact on US bonds will be great, i.e. Duration is greater. Again, try it in Excel if you fancy proving it to yourself.
So, remember, which bonds have higher duration?
Longer maturity
Lower coupon
Lower rate environments.
Start learning the core skills you’ll need in the world of investment banking with our free Investment Banking Fundamentals course, drawing in core modules from our wider course catalogue to get you started on a career in finance.