Perpetuities: Definitions, Concepts and Examples
Perpetuities are an important concept in corporate finance and investment analysis. A perpetuity is a constant stream of cash flows that continues indefinitely into the future. Understanding perpetuities allows financial analysts to properly value assets and investment opportunities that involve long-term, ongoing cash flows. They are one the most fundamental tools in valuation alongside concepts such as yield curves and zero-coupon bonds.
Article Contents
Key Takeaways
|
Aspect |
Takeaway |
| Definition | A perpetuity is a constant stream of cash flows continuing indefinitely into the future |
| Formula | The formula for valuing a perpetuity is: Present Value = Cash flow per period / Discount rate |
| Discount Rate | The discount rate reflects the time value of money and associated investment risks |
| Growing Perpetuities | Growing perpetuities have cash flows that increase at a constant growth rate each period |
| Comparison to Annuities | Perpetuities continue forever while annuities have a fixed number of payment periods |
| Applications | Perpetuities are used to value financial assets with very long or infinite lives |
| Examples | Examples of perpetuity valuation include stocks, bonds, royalties, real estate, settlements |
| Key Assumptions | Key assumptions are constant discount rate and growth rate, which may not hold true |
| Synonyms | Perpetuity and forever mean the same thing – an unlimited time period |
What is a Perpetuity?
A perpetuity is a stream of cash flows that continues forever without end. The equal periodic payments can occur at any fixed interval, such as monthly, quarterly or annually. A key feature is that the perpetual cash flows remain constant over time. Their present value and theoretical fair value can be calculated using a standard perpetuity formula.
Perpetuity Formula and Calculation
The formula for the present value (PV) of a perpetuity is:
PV of Perpetuity = Cash flow per period / Discount rate
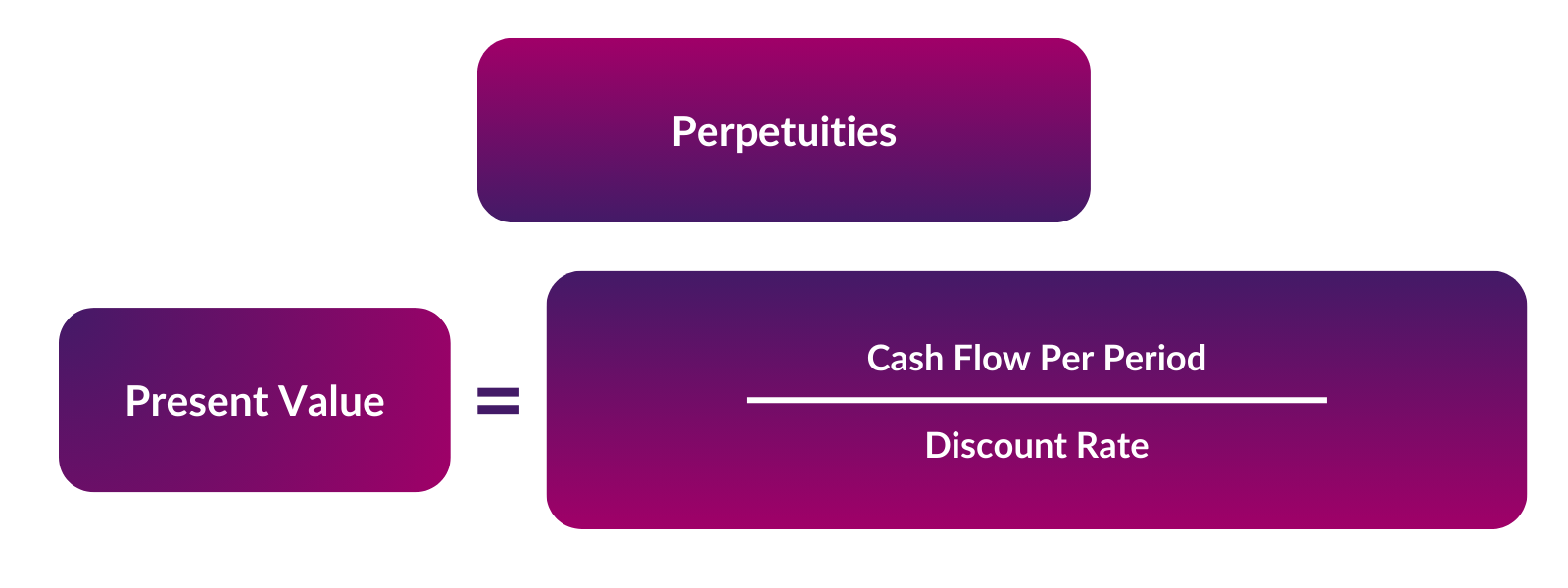
Where:
- Cash flow per period = The fixed periodic payment amount
- Discount rate = The interest rate used to discount the perpetuity to present value
For example, if a perpetual bond pays $100 annually, and the discount rate is 5%, the present value is:
- PV of Perpetuity = $100 / 0.05 = $2,000
This means an investor should be willing to pay $2,000 today to receive $100 every year forever, assuming a 5% discount rate. The lower the interest rate, the higher the present value of the perpetuity.
The discount rate is a critical component in perpetuity valuation. It reflects the time value of money and is typically influenced by factors like the risk-free interest rate, market conditions, and specific risks associated with the cash flow. For instance, a higher discount rate is used for riskier cash flows, which lowers the present value of the perpetuity.
Growing Perpetuities: Extending the Concept
A variation on a standard perpetuity is a growing perpetuity, where instead of fixed cash flows, the periodic payments increase at a constant growth rate. The formula for a growing perpetuity PV is:
PV = C / (r – g)
Where:
- C = Initial cash flow
- r = Discount rate
- g = Growth rate
For example, if the initial cash flow is $100, and payments grow at 3% annually at a 5% discount rate, the PV is:
PV = $100 / (0.05 – 0.03) = $5,000
With a growth rate of 4%, the value of the perpetuity would rise to $10,000.
This shows how faster growth can increase the present value of a perpetuity versus flat or slowly growing cash flows.
Perpetuity vs Annuity: A Comparative Analysis
Perpetuities and annuities, while similar, differ mainly in their length.
Perpetuities have infinite payments, while annuities have a fixed number of payment periods.
One key assumption in perpetuity valuation is that the discount rate is constant over time, which might not hold in dynamic market conditions. Similarly, growing perpetuities assume a constant growth rate, an assumption that may not always reflect real-world scenarios.
For example, with an ordinary annuity certain, payments are made for a set term like 20 years. But a perpetuity continues making equal payments forever into the infinite future.
Their formulas also differ accordingly, with perpetuities using a simple 1/r discount rate divisor and annuities using a discounted cash flow approach based on the total number of periods. Still, both tools serve a similar purpose in determining the present value of future cash flow streams.
Practical Applications of Perpetuity in Finance
Perpetuities have many practical applications in corporate finance and investment analysis:
- Valuing shares using discounted cash flow After an explicit forecast of cashflows for 5-7 years, subsequent cashflows are valued as a perpetuity growing at typically 1-2.5%
- Pricing acquisitions based on long term royalty rights
- Valuing bonds and preferred shares with no maturity date
- Evaluating commercial real estate. A commercial property is typically valued as a perpetuity based on the current rent as the “first payment”
- Analysing the present value of structured settlements and lottery payouts.
In these cases, being able to accurately value cash flows continuing far out into the future is critical.
The perpetuity concept and related formulas are important tools financial analysts rely on to properly value these kinds of long-term assets and cash flow streams.
In summary, perpetuities represent future cash flow streams continuing indefinitely. Their valuation relies on a simple, straightforward formula using the constant periodic payment divided by the discount rate.
Perpetuities are useful in finance for analysing assets with very long or infinite lives. Understanding the perpetuity concept is key for corporate analysts and investors looking to properly value long-term equity dividends, bonds, royalties, annuities, and various other assets and cash flows.
A note to be wary of is that textbooks will show two different formats of the formula, where:
- The first payment happens at the date of valuation
- Where it happens at the end of the first period
The latter is the standard one used in finance, while our formulae is standard for the valuation of a perpetuity today, where the first payment happens one time-period (a year, quarter etc) from now.

