Time Value of Money (TVM): Examples, Relevant Formulas and Interpretation
Time Value of Money (TVM) is a core corporate finance concept that refers to the principle that money available now is worth more than the same amount in the future, due to its potential earning capacity today. The TVM concept underlies all calculations and decisions involving time and interest rates in both business and personal finance. Understanding TVM is crucial for corporate finance professionals and investors to properly evaluate cash flows that occur at different points in time.
Article Contents
Key Takeaways
| Concept | Key Takeaways |
| Time Value of Money (TVM) | – Money available earlier is worth more than the same amount later due to earning capacity.
– TVM underlies calculations/decisions involving time and interest rates. – Critical concept in corporate finance and investing. |
| TVM Calculations | – Present Value (PV)
– Future Value (FV) – Net Present Value (NPV) – Internal Rate of Return (IRR) |
| Importance of TVM | – Enables comparison of cash flows over time.
– Evaluates long-term projects. – Determines if investments have positive value. |
| TVM and Inflation | – Inflation reduces purchasing power over time.
– Use real interest rates and cash flows to account for inflation. |
| Applications of TVM | – Capital budgeting, valuation, stocks, bonds, risk management, retirement planning. |
| Advanced Concepts | – Compounding periods impact returns.
– Continuous compounding used in certain models. |
What is Time Value of Money?
The time value of money concept can be seen more clearly when looking at the formula for future value:
FV = PV x (1+r)^n
Where:
- FV = Future Value
- PV = Present Value
- r = Interest rate per period
- n = Number of periods
This formula calculates how an amount of money today (PV) can earn interest over time at a specified rate, resulting in a future value (FV) amount. The longer the time period and higher the interest rate, the higher the future value.
For example, $100 invested today at an annual interest rate of 5% for 10 years would result in a future value of $162.89.
This demonstrates that $100 today is worth more than $100 ten years later, because the money today can be invested to start earning interest immediately and be worth more in ten years time.
Time Value of Money Calculations
There are four key calculations used in corporate finance where the TVM concept is utilised:
- Present Value (PV) – The current worth of a future sum of money.
- Future Value (FV) – The value of a sum of money at a given point in the future.
- Net Present Value (NPV) – The difference between the present value of cash inflows and present value of cash outflows over time. A positive NPV indicates a good investment.
- Internal Rate of Return (IRR) – The interest rate at which the NPV of future cash flows equals the initial investment. Described another way, the IRR is the annual growth of an initial investment equivalent to a given a set of future cash flows, therefore a higher IRR indicates a more desirable investment.
Why is TVM Important?
Understanding the time value of money concept is crucial in corporate finance for several reasons:
- TVM allows apples-to-apples comparison of cash flows at different times using discounting and compounding techniques.
- TVM enables businesses to evaluate long-term projects with cash flows over differing time periods.
- Calculating NPV and IRR using the TVM concept determines if an investment has a positive economic value and an acceptable return rate to proceed.
In summary, TVM is a fundamental corporate finance concept underlying many analyses and decisions. Managers need a firm grasp of TVM to make sound long-term financial choices and properly value potential investment opportunities.
TVM and Inflation
Inflation, or the tendency for the prices of goods/services to increase over time, impacts the time value of money. As inflation rises, the purchasing power of money decreases.
To account for inflation, calculations involving the TVM concept may use a real interest rate alongside real cash flows. The real rate is the nominal interest rate minus the inflation rate, whilst real cash flows will also exclude any inflationary impact. Being consistent with type of rate used and the cash flows used ensures TVM calculations reflect the real purchasing power of the cash flows over time. This is crucial for obtaining an accurate picture of investment worth and returns.
For example, with 5% inflation and 6% nominal interest rate, a 1% real interest rate can be used in TVM based calculations alongside cash flows that have been adjusted to exclude the impact of inflations. Failing to account for inflation consistently can lead to poor financial modelling and uneconomic investment decisions.
Applications of TVM in Finance
Time value of money has many applications in corporate finance:
- Capital Budgeting – TVM based methods like NPV and IRR are used to evaluate project cash flows and decide which investments are economically viable.
- Business Valuation – TVM helps determine the fair value of a business based on future expected free cash flows to the firm.
- Stocks/Bonds – The concepts of present value and required return are applied to valuing stocks, bonds, and calculating yields to maturity.
- Risk Management – TVM concepts enables companies to model various risk scenarios and stress test financial outcomes based on different discount rates.
- Retirement Planning – TVM helps assess savings growth requirements and portfolio returns needed to achieve retirement goals.
Overall, time value of money concepts are commonly applied in corporate financial modelling, valuation, risk management, and long-term decision making.
Advanced TVM Concepts
Understanding Different Compounding Periods
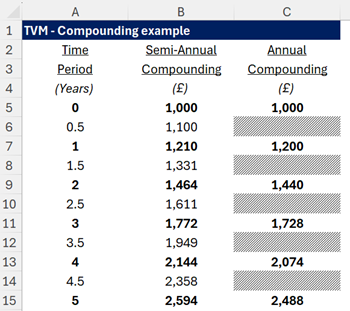
The Time Value of Money calculations often vary based on the frequency of compounding. Whether interest is compounded annually, semi-annually, quarterly, or monthly, it significantly impacts the final amount. For example, £1,000 invested at an annual interest rate of 20% compounded semi-annually (i.e. 10% every six months) will yield a different value than if it were compounded annually. This is because more frequent compounding periods result in interest being calculated on interest more often.
Continuous Compounding
A more complex extension of the above concept is continuous compounding, where interest is calculated and added to the principal at every possible instant. The formula for continuous compounding is FV = PV * e^(rt), where e is the base of the natural logarithm, r is the annual interest rate, and t is the time in years. This concept is particularly relevant in certain financial models and theoretical scenarios.
Real-World Examples of Time Value of Money
Here are some real-world examples that demonstrate the time value of money principle:
- Early Retirement Offers: Companies may offer greater upfront incentives for employees to take early retirement packages versus staying longer for the standard package value. This reflects the high present value of near-term payouts.
- Structured Settlements: Lawsuits or insurance claims are often settled by structured payments over time rather than a single lump sum. This takes advantage of the time value of money by deferring the payment obligations, thus paying less in present value terms.
- Lottery Winnings: Lottery winners can choose between long-term installment payments or a one-time present cash value amount. The lump sum is lower than total installments to account for TVM.
- Zero Coupon Bonds: These bonds are sold at a discount to par value and do not pay periodic interest. The discount reflects the time value difference between present price paid and future redemption value.
- Annuities: Annuity issuers leverage the concept of present value of future payments to offer periodic income for life in retirement.
In summary, the time value of money is universally applicable across finance. Corporations, governments, financial institutions, and individuals all leverage the power of TVM in modelling, valuation, markets, and decision making. A thorough understanding of this concept is essential for all finance professionals and managers.
To learn more about Compound Annual Growth Rates and other financial metrics, take our Financial Maths Bootcamp course.

