Annual Percentage Rate (APR): Definitions, Formulas and Examples
Annual Percentage Rate (APR) or “Effective Annual Rate” is an important concept in retail lending. It represents the true yearly cost of borrowing money or obtaining credit, expressed as a percentage rate. By understanding APR, borrowers can compare the total cost of loans and make informed decisions.
Article Contents
Key Takeaways
| Takeaway | Description |
|---|---|
| APR Definition | APR represents the true yearly cost of borrowing money or obtaining credit, expressed as a percentage rate. It accounts for the interest rate as well as other associated fees and charges. |
| APR Calculation | The APR can be calculated using the RATE function in Excel, which accounts for compounding frequency. The formula is: =RATE(n,-payment,principal)*12, where n is the number of payment periods, payment is the monthly payment, and principal is the loan amount. |
| Uses of APR | APR is required to be disclosed by regulators for retail lending products like mortgages, credit cards, and auto loans. It allows borrowers to compare the total cost of different loan options. |
| Limitations of APR | APR has some limitations, including ignoring the time value of money, not accounting for variable interest rates, and not considering opportunity costs or changes in financial behavior. |
| APR vs. IRR | In the realm of retail lending, IRR (Internal Rate of Return) is used instead of APR to measure the yield on investments. |
| Good APR Rates | A desirable APR rate depends on the financial product and prevailing market conditions. Credit cards typically have the highest APRs, often over 25%, while other loans should be evaluated based on current benchmark lending rates. |
What is Annual Percentage Rate?
Annual Percentage Rate (APR) is the annualized interest rate charged on a loan or earned on an investment. But it’s more than just the interest. The APR factors in not only the interest rate but also other costs associated with obtaining the loan or making the investment, such as origination fees, broker fees, and other charges.
APR is designed to give borrowers and investors an accurate picture. By accounting for compounding interest, fees, and other charges, it allows for a straightforward comparison between different financial products. A rule of thumb: a higher APR often indicates a more expensive loan or a lower-yielding investment, and vice versa for a lower APR.
How to Calculate APR in Excel
Excel offers a handy function for APR calculation. The RATE function can be used to determine the APR for a given loan or investment. For instance, for a $10,000 loan at 5% interest with 12 monthly payments of $873.21, the APR would be:
=RATE(12,-873.21,10000)*12

This formula returns an APR of 8.72%. The magic of the RATE function lies in its ability to account for compounding frequency. RATE calculates the rate earned each payment period. For monthly payments it calculates a monthly rate – multiplying by 12 gives us an effective annual rate.

Uses of APR in Retail Lending
Stating an APR is usually required by regulators when companies make loans to retail borrowers, for example mortgages, credit cards and car (auto) loans. Regulators are concerned to make sure that potential borrowers have an accurate measure of “All -in” cost after taking account of fees and unusual interest calculation methods: typically banks charge simple interest, i.e. if you borrow for 3 months you pay interest = 90/365* annual rate. On a credit card interest is calculated and compounds daily. The simple annual rate for my credit card is 24.3080%. The “Effective Annual Rate” after taking account of daily compounding is 27.21%.
Credit card companies quote a “typical” or “representative” APR in their advertising. This typical rate means that more than 50% of their customers pay below this rate. The reason they cannot quote an actual figure is that individual customers will be charged different rates depending upon their credit scores.
In the realm of retail lending, IRRs take the place of APR.
Limitations of Annual Percentage Rate
While the Annual Percentage Rate provides a useful measure to compare the cost of loans and the yield of investments, it is not without its limitations, and being mindful of these is crucial for balanced financial decision-making.
- Ignoring Time Value of Money: APR doesn’t account for the time value of money, meaning it doesn’t consider the diminishing purchasing power of money over time. This can potentially understate the cost of longer-term loans.
- Overlooking Loan Duration: APR can potentially mislead in scenarios where loans have different durations. Two loans may have the same APR but differing total costs if they are to be repaid over different periods.
- Variable Rates: For loans or credit cards with variable interest rates, the APR can only provide a snapshot based on current rates. In such instances, future rate increases can render low initial APRs somewhat misleading.
- Ignoring Financial Behaviour: The actual cost or yield of a loan or investment might differ from the APR if a borrower or investor’s behaviour changes, such as making late payments or withdrawing early from an investment, which could incur additional fees or penalties.
- Not Accounting for Opportunity Costs: APR fails to account for the opportunity cost of choosing one loan or investment over another. Even if a particular option has a lower APR, it may not necessarily be the most financially prudent choice in the broader context of an individual’s or company’s financial landscape.
- Different Calculations: Sometimes, the way APR is calculated can vary between financial institutions and products, making it challenging to make precise comparisons between different offerings.
Exercises and Examples for Calculating APR
Let’s look at some examples for hands-on practice:
Exercise 1
A loan has 0.48% stated interest, 18 monthly payments of $166.73, and a $150 origination fee. What is the APR?
Solution
- Initial Loan Balance = $3000
- APR = RATE(18,-166.73,3000-150)*12 = 6.596%
The impact of the fee is to reduce the balance received by 5%. This dramatically increases the effective cost.
Exercise 2
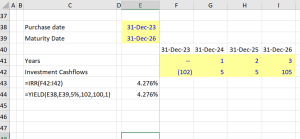
A bond investment yields 5% annually over 3 years but charges a 2% upfront fee. What is the APR?
Solution
- Interest Earned = 5% * 3 years = 15%
- Net Interest After Fee = 15% – 2% = 13%
- Number of Periods = 3 years
For this bond-like investment, there is a simple approximate formula we can use: APR = Net Interest / Number of Periods = 13% / 3 = 4.33%
Excel has the specific function YIELD() to calculate an exact result, which gives the same result as =IRR() for the simple case of a bond like investment held to maturity over its 3-year life. Both these formulae give the more accurate, but slightly lower figure of 4.276%
To learn more about APR and other financial metrics in retail lending, check out our financial maths elearning course.


